
- Tác giả Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:55.
- Sửa đổi lần cuối 2025-01-22 17:47.
Trong một hình thoi tất cả các cạnh bên bằng nhau và các cạnh đối diện song song. Hơn nữa a hình thoi cũng là một hình bình hành và do đó thể hiện các thuộc tính của một hình bình hành và điều đó các đường chéo của một hình bình hành phân giác nhau.
Tương ứng, các đường chéo của một hình thoi có phân giác nhau không?
Trong bất kỳ hình thoi , NS đường chéo (đường liên kết các góc đối diện) chia đôi nhau vuông góc (90 °). Đó là, mỗi đường chéo cắt khác thành hai phần bằng nhau và góc mà chúng giao nhau luôn là 90 độ. Trong hình trên, kéo bất kỳ đỉnh nào để định hình lại hình thoi và thuyết phục bản thân của bạn rằng điều này là như vậy.
Thứ hai, các đường chéo của hình thoi có vuông góc với nhau không? Thuộc tính của một Hình thoi Các đường chéo là vuông góc đến và chia đôi nhau. Các góc kề là phụ (Ví dụ: ∠A + ∠B = 180 °). MỘT hình thoi là một hình bình hành ai đường chéo là vuông góc cho nhau.
Lưu ý điều này, làm thế nào bạn chứng minh được các đường chéo của một hình thoi là các đường phân giác vuông góc?
Bằng chứng rằng các đường chéo của hình thoi vuông góc với nhau Tiếp tục ở trên bằng chứng : Các phần tương ứng của tam giác đồng dư là đồng dư, do đó cả 4 góc (góc ở giữa) đều đồng dư. Điều này dẫn đến thực tế là tất cả chúng đều bằng 90 độ và đường chéo là vuông góc cho nhau.
Hình thoi có phải là hình bình hành không?
ĐỊNH NGHĨA: A hình thoi là một hình bình hành với bốn mặt đồng dư. LÝ THUYẾT: Nếu a hình bình hành là một hình thoi , mỗi đường chéo chia đôi một cặp góc đối diện. THEOREM Converse: Nếu a hình bình hành có đường chéo phân giác một cặp góc đối diện, nó là một hình thoi.
Đề xuất:
Các đường chéo của hình vuông có bằng nhau không?
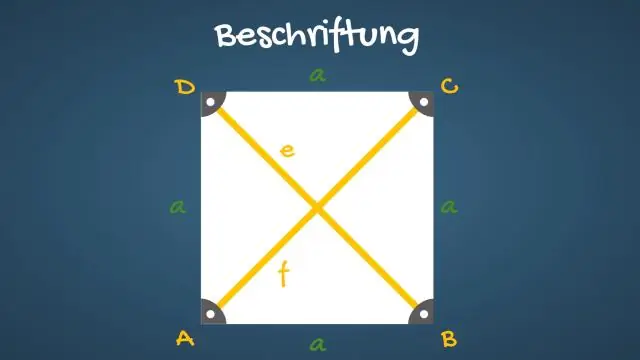
Các đường chéo của một hình vuông chia đôi các góc của nó. Các cạnh đối diện của hình vuông song song và có độ dài bằng nhau. Cả bốn cạnh của một hình vuông đều bằng nhau. Các đường chéo của một hình vuông bằng nhau
Các đường chéo luôn phân giác nhau trong một hình bình hành?
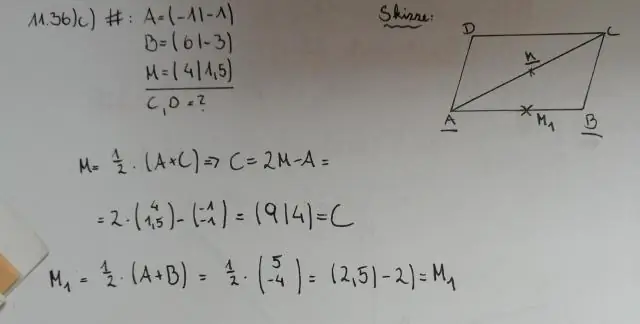
Trong bất kỳ hình bình hành nào, các đường chéo (đường nối các góc đối diện) phân giác nhau. Tức là mỗi đường chéo sẽ cắt đường chéo kia thành hai phần bằng nhau. Trong hình trên, kéo bất kỳ đỉnh nào để định hình lại hình bình hành và tự thuyết phục bạn rằng đây là như vậy
Các đường chéo của hình bình hành có phân giác nhau bằng 90 không?

Trong bất kỳ hình thoi nào, các đường chéo (đường nối các góc đối diện) phân giác nhau thành các góc vuông (90 °). Nghĩa là, mỗi đường chéo cắt đường chéo kia thành hai phần bằng nhau và góc mà chúng cắt nhau luôn là 90 độ
Những hình bình hành nào có hai đường chéo phân giác nhau?
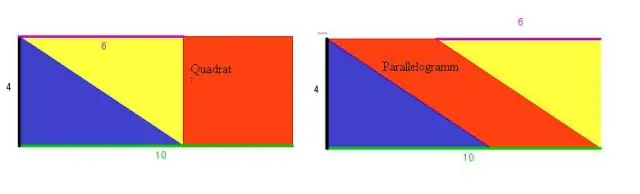
Nếu hai cạnh kề của hình bình hành bằng nhau thì đó là hình thoi. Phép thử này thường được coi là định nghĩa của hình thoi. Một tứ giác có các đường chéo phân giác các góc vuông với nhau là một hình thoi
Đường chéo của một góc vuông có phải là đường phân giác không?

Hình vuông có các tính chất sau: Tất cả các tính chất của hình thoi đều được áp dụng (các tính chất quan trọng ở đây là các cạnh song song, đường chéo là đường phân giác vuông góc của nhau và đường chéo phân giác các góc). Tất cả các thuộc tính của hình chữ nhật đều được áp dụng (điều duy nhất quan trọng ở đây là các đường chéo là đồng dư)
