- Tác giả Lynn Donovan [email protected].
- Public 2023-12-15 23:55.
- Sửa đổi lần cuối 2025-01-22 17:46.
BFS viết tắt của Tìm kiếm đầu tiên theo chiều rộng . DFS viết tắt của Tìm kiếm sâu đầu tiên . 2. BFS ( Tìm kiếm đầu tiên theo chiều rộng ) sử dụng cấu trúc dữ liệu Hàng đợi để tìm đường đi ngắn nhất. BFS có thể được sử dụng để tìm đường dẫn ngắn nhất nguồn duy nhất trong một biểu đồ không trọng số, bởi vì trong BFS , chúng ta đạt đến một đỉnh có số cạnh tối thiểu từ một đỉnh nguồn.
Ở đây, tìm kiếm theo chiều sâu với ví dụ là gì?
Tìm kiếm sâu hơn đầu tiên hoặc DFS cho một Đồ thị. Độ sâu Truyền tải đầu tiên (hoặc Tìm kiếm ) cho một biểu đồ tương tự như Độ sâu Truyền tải đầu tiên của một cái cây. Vì thí dụ , trong biểu đồ sau, chúng tôi bắt đầu đi ngang qua từ đỉnh 2. Khi đến đỉnh 0, chúng ta nhìn cho tất cả các đỉnh liền kề của nó. 2 cũng là một đỉnh kề của 0.
Ngoài phần trên, tìm kiếm theo độ sâu đầu tiên trả lại gì? Các chiều sâu - tìm kiếm đầu tiên thuật toán cho phép chúng ta xác định xem hai nút, nút x và nút y, có đường đi giữa chúng hay không. Thuật toán DFS làm điều này bằng cách xem xét tất cả các nút con của nút bắt đầu, nút x, cho đến khi nó đến nút y.
Tương tự, tìm kiếm đầu tiên theo chiều rộng là gì?
Tìm kiếm đầu tiên theo chiều rộng (BFS) Thuật toán Tìm kiếm đầu tiên theo chiều rộng là một đồ thị đi ngang qua thuật toán bắt đầu duyệt qua đồ thị từ nút gốc và khám phá tất cả các nút lân cận. Sau đó, nó chọn nút gần nhất và khám phá tất cả các nút chưa được khám phá.
Việc sử dụng tìm kiếm độ sâu đầu tiên là gì?
Chiều sâu - tìm kiếm đầu tiên được sử dụng trong sắp xếp tôpô, lập lịch các bài toán, phát hiện chu trình trong đồ thị và giải các câu đố chỉ với một giải pháp, chẳng hạn như mê cung hoặc câu đố sudoku. Các ứng dụng khác liên quan đến việc phân tích mạng, ví dụ, kiểm tra xem một biểu đồ có phải là lưỡng phân hay không.
Đề xuất:
Cắm tiện ích mở rộng vào tiện ích mở rộng có nguy hiểm không?

Bạn có thể cắm dây mở rộng vào một dây mở rộng khác không? Một lần nữa, về mặt kỹ thuật thì bạn có thể làm được, nhưng nó không được khuyến khích, vì nó được coi là một mối nguy hiểm hỏa hoạn. Khi bạn bắt đầu thêm dây nối dài, bạn có nguy cơ làm cho thiết bị của bạn chạy quá lâu và thiếu năng lượng - không an toàn
Các công cụ tìm kiếm tìm kiếm các công cụ tìm kiếm khác là gì?
Để bắt đầu cuộc phiêu lưu tìm kiếm của chúng tôi, hãy xem xét một số công cụ tìm kiếm chung ngoài ba công cụ hàng đầu. DuckDuckGo. Lo ngại về quyền riêng tư trực tuyến? Tìm kiếm Mã hóa. Tìm kiếm một giải pháp thay thế cho DuckDuckGo? Ecosia. Muốn trồng cây trong khi bạn tìm kiếm? Kho lưu trữ. Blekko. WolframAlpha. Gigablast. Tìm kiếm trên Facebook
Tìm kiếm đầu tiên theo chiều rộng trong trí tuệ nhân tạo là gì?
Được xuất bản vào ngày 4 tháng 4 năm 2017. Tìm kiếm theo chiều rộng-đầu tiên giống như đi ngang qua một cái cây trong đó mỗi nút là một trạng thái có thể là một ứng cử viên tiềm năng cho giải pháp. Nó mở rộng các nút từ gốc của cây và sau đó tạo ra từng cấp độ của cây tại một thời điểm cho đến khi tìm ra giải pháp
Làm cách nào để căn giữa văn bản theo chiều dọc và Div theo chiều ngang?
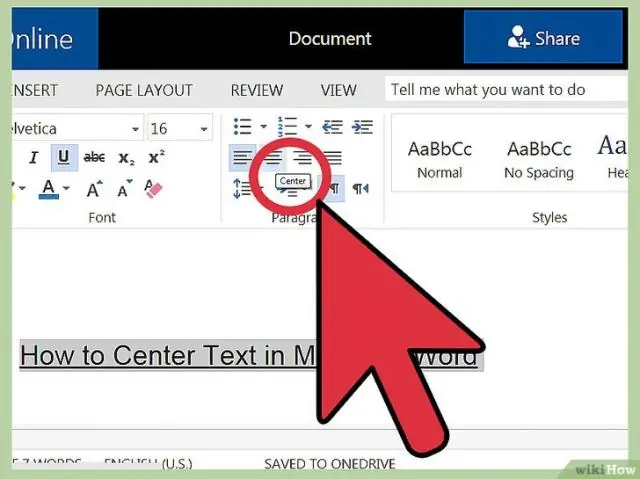
Để căn chỉnh theo chiều dọc, hãy đặt chiều rộng / chiều cao của phần tử mẹ thành 100% và thêm display: table. Sau đó, đối với phần tử con, hãy thay đổi hiển thị thành table-cell và thêm vertical-align: middle. Để căn giữa theo chiều ngang, bạn có thể thêm text-align: center để căn giữa văn bản và bất kỳ phần tử con nội dòng nào khác
Trường hợp nào viết hoa chữ cái đầu tiên của từ đầu tiên trong mỗi câu?

Hộp kiểm tra Viết hoa chữ cái đầu tiên của câu được chọn theo mặc định. Khi nó được chọn, Visio viết hoa chữ cái đầu tiên của bất kỳ từ nào sau dấu chấm, dấu xuống dòng, dấu chấm phẩy hoặc bản tin đầu tiên của bất kỳ từ nào trong danh sách hoặc cột bảng
