
- Tác giả Lynn Donovan [email protected].
- Public 2023-12-15 23:55.
- Sửa đổi lần cuối 2025-01-22 17:46.
Danh tính cho phép chúng tôi đơn giản hóa các biểu thức phức tạp. Chúng là những công cụ cơ bản của lượng giác dùng trong giải phương trình lượng giác , cũng giống như tính toán, tìm mẫu số chung và sử dụng các công thức đặc biệt là những công cụ cơ bản của giải quyết đại số phương trình.
Sau đó, điều gì làm cho một phương trình lượng giác trở thành một đồng nhất?
Trong toán học, nhận dạng lượng giác là sự bình đẳng liên quan đến lượng giác các hàm và đúng với mọi giá trị của các biến số xảy ra trong đó cả hai vế của đẳng thức đều được xác định. Về mặt hình học, đây là danh tính liên quan đến các chức năng nhất định của một hoặc nhiều góc.
Cũng Biết, phương trình lượng giác là gì? MỘT phương trình lượng giác là bất kỳ phương trình chứa một lượng giác hàm số. Như đã đề cập trong Lượng giác Danh tính, một phương trình lượng giác điều đó đúng với bất kỳ góc nào được gọi là lượng giác xác thực. Có khác phương trình Tuy nhiên, điều đó chỉ đúng với một số góc độ nhất định.
Tương tự, người ta có thể hỏi, cách dễ nhất để giải các phép đồng dạng lượng giác là gì?
BƯỚC 1: Chuyển đổi tất cả sec, csc, cot và tan thành sin và cos. Hầu hết điều này có thể được thực hiện bằng cách sử dụng thương số và tương hỗ danh tính . BƯỚC 2: Kiểm tra tất cả các góc để tìm tổng và chênh lệch và sử dụng danh tính để loại bỏ chúng. BƯỚC 3: Kiểm tra các bội số của góc và loại bỏ chúng bằng các công thức thích hợp.
Sin 2x bằng gì?
sin2x =( tội x) 2 = 12 (1 − cos ( 2x )).
Đề xuất:
Tại sao diode Schottky lại hữu ích cho việc chỉnh lưu tần số cao?
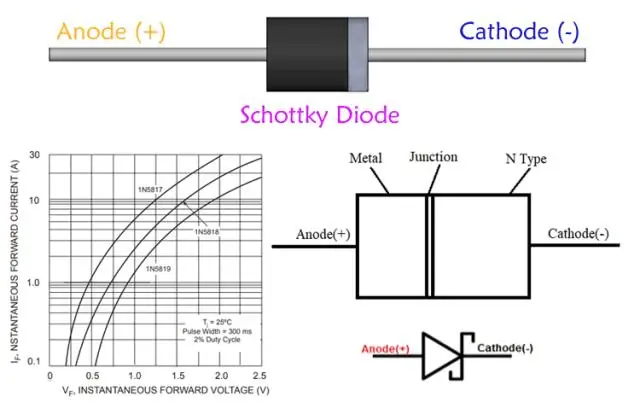
Các ứng dụng diode Schottky. Bộ chỉnh lưu: Điốt Schottky cũng được sử dụng như bộ chỉnh lưu công suất cao. Mật độ dòng điện cao của chúng và giảm điện áp chuyển tiếp chậm có nghĩa là ít điện năng bị lãng phí hơn nếu sử dụng điốt tiếp giáp PN thông thường. Schottkydiodes có xu hướng có dòng điện rò rỉ ngược cao
Tại sao tư duy phản biện lại quan trọng trong việc giải quyết vấn đề?

Giải quyết vấn đề và tư duy phản biện đề cập đến khả năng sử dụng kiến thức, dữ kiện và dữ liệu để giải quyết vấn đề một cách hiệu quả. Nhân viên lý tưởng có thể suy nghĩ chín chắn và sáng tạo, chia sẻ suy nghĩ và ý kiến, sử dụng khả năng phán đoán tốt và đưa ra quyết định
Tại sao trình chống phân mảnh ổ đĩa lại hữu ích?

Chống phân mảnh giống như dọn dẹp nhà cửa cho PC của bạn, nó thu thập tất cả các phần dữ liệu nằm rải rác trên ổ cứng của bạn và đặt chúng lại với nhau một lần nữa. Tại sao chống phân mảnh lại quan trọng? Bởi vì mọi máy tính đều phải chịu sự phát triển liên tục của sự phân mảnh và nếu bạn không dọn dẹp nhà cửa, PC của bạn sẽ bị
Tại sao chất lượng dữ liệu lại quan trọng đối với việc thu thập dữ liệu thống kê?

Dữ liệu chất lượng cao sẽ đảm bảo hiệu quả hơn trong việc thúc đẩy thành công của công ty vì sự phụ thuộc vào các quyết định dựa trên thực tế, thay vì trực giác của con người hoặc thói quen. Tính đầy đủ: Đảm bảo không có khoảng trống trong dữ liệu từ những gì được cho là được thu thập và những gì đã thực sự được thu thập
Tại sao Liên kết động lại quan trọng trong việc triển khai tính đa hình?

Liên kết động cho phép một lệnh gọi hàm thành viên được giải quyết tại thời điểm chạy, theo kiểu thời gian chạy của một tham chiếu đối tượng. Điều này cho phép mỗi lớp do người dùng xác định trong hệ thống phân cấp kế thừa có một cách triển khai khác nhau của một chức năng cụ thể
